Arithmetic Aptitude :: Logarithm
-
Which of the following statements is not correct?
-
\( \frac { log\sqrt{8} } { log8 } \)is equal to:
-
If log\( \frac {a} {b } \)+log\( \frac {b} {a } \)=log (a + b), then
-
If log10 7 = a, then log10\([ \frac { 1 } { 70 }] \)is equal to:
-
If log10 2 = 0.3010, then log2 10 is equal to:
-
The value of\([\frac { 1 } { log^360 }+€‹€‹\)\([\frac { 1 } { log^460 }+€‹€‹\)\([\frac { 1 } { log^560 }]\)is
-
If logx\([\frac { 9 } {16 } ]=\)\(-[\frac { 1 } {2 } ],\)then x is equal to:
-
If ax = by, then:
Whatsapp
Facebook
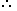log (2 + 3) 
log (2 x 3)(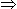
log (33 ) = 1.431