Arithmetic Aptitude :: Logarithm
Logarithm:
If a is a positive real number, other than 1 and am = x, then we write:
m = logax and we say that the value of log x to the base a is m.
Examples:
(i). 103 1000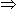 
log10 1000 = 3.
(ii). 34 = 81 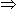log3 81 =
(iii) 2-3 = \(\frac { 1 } { 8} \) 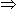log2 \(\frac { 1 } { 8} \)= -3
(iv) (.1)2 = .01 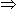log(.1) .01 = 2.
2.Properties of Logarithms:
1. loga (xy) = loga x + loga y
2. logx x = 1
3 .loga 1 = 0
4. loga (xn) = n(loga x)
5. loga \([ \frac { x } { y } ]\) = loga x - loga y
6 . loga x = \( \frac { logb X } { logb a} \) = \( \frac { log X } { log a} \)