Civil Engineering :: Theory of Structures
-
If a concrete column 200 x 200 mm in cross-section is reinforced with four steel bars of 1200 mm2 total cross-sectional area. Calculate the safe load for the column if permissible stress in concrete is 5 N/mm2 and Es is 15 Ec
-
If normal stresses due to longitudinal and transverse loads on a bar are σ1 and σ2 respectively, the normal component of the stress on an inclined plane θ° to the longitudinal load, is
-
A shaft subjected to a bending moment M and a torque T, experiences
-
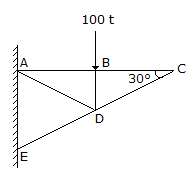
In the truss shown in given figure the force in member DC is
-
If M, I, R, E, F, and Y are the bending moment, moment of inertia, radius of curvature, modulus of elasticity stress and the depth of the neutral axis at section, then
-
The eccentricity (e) of a hollow circular column, external diameter 25 cm, internal diameter 15 cm for an eccentric load 100 t for non-development of tension, is
-
If Ix and Iy are the moments of inertia of a section about X and Y axes, the polar moment of inertia of the section, is
-
Maximum shear stress theory for the failure of a material at the elastic limit, is known
-
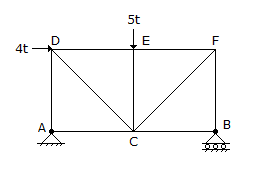
The force in AC of the truss shown in the given figure, is
-
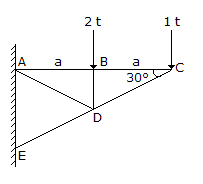
For determining the force in the member AB of the truss shown in the given figure by method of sections, the section is made to pass through AB, AD and ED and the moments are taken about


 Whatsapp
Whatsapp
 Facebook
Facebook

