Civil Engineering :: Theory of Structures
-
The assumption in the theory of bending of beams, is :
-
In case of principal axes of a section
-
The shape factor of standard rolled beam section varies from
-
Shear strain energy theory for the failure of a material at elastic limit, is due to
-
The maximum deflection due to a load W at the free end of a cantilever of length L and having flexural rigidity EI, is
-
The point of contraflexure is the point where
-
The normal component of a force inclined through θ° is obtained by multiplying the force by
-
A material which obeys Hook's law, is subjected to direct stress σ0. At its elastic limit, the following statement is true,
-
In the truss shown in the given figure, the force in member BC is
-
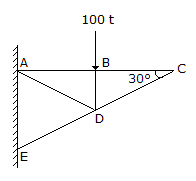
In case of principal axes of a section
Whatsapp
Facebook
