Civil Engineering :: Theory of Structures
-
Ab and Ac are the cross sections of bronze and copper bars of equal length, σb, σc are their respective stresses due to load P. If Pb and Pc are the loads shared by them, (where Eb and Ec are their modulii)
-
A compound truss may be formed by connecting two simple rigid frames, by
-
The locus of the end point of the resultant of the normal and tangential components of the stress on an inclined plane, is
-
The degree of indeterminacy of the frame in the given figure, is
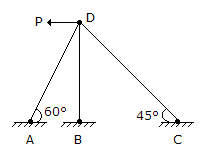
-
The equivalent length of a column of length L having one end fixed and the other end free, is
-
To determine the force in BD of the truss shown in the given figure a section is passed through BD, CD and CE, and the moments are taken about
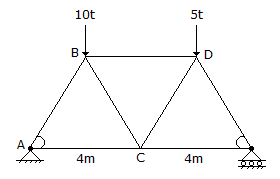
-
The ratio of the length and depth of a simply supported rectangular beam which experiences maximum bending stress equal to tensile stress, due to same load at its mid span, is
-
The radius of gyration of a rectangular section (depth D, width B) from a centroidal axis parallel to the width is
-
For a strongest rectangular beam cut from a circular log, the ratio of the width and depth, is
-
The moment of inertia of a circular section about any diameter D, is


 Whatsapp
Whatsapp
 Facebook
Facebook

