GATE 2017-2018 :: GATE Mathematics
-
Let c00 be the vector space of all complex sequences having finitely many non-zero terms. Equip c00 the inner product 〈x, y〉 =
 for all x=(xn) and y=(yn) in c00. Define f: c00 → ℂ by f(x)=
for all x=(xn) and y=(yn) in c00. Define f: c00 → ℂ by f(x)= 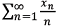 . Let N be the kernel of f.Which of the following is FALSE?
. Let N be the kernel of f.Which of the following is FALSE? -
Let c00 be the vector space of all complex sequences having finitely many non-zero terms. Equip c00 the inner product 〈x, y〉 =
 for all x=(xn) and y=(yn) in c00. Define f: c00 → ℂ by f(x)=
for all x=(xn) and y=(yn) in c00. Define f: c00 → ℂ by f(x)= 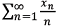 . Let N be the kernel of f.Which of the following is FALSE?
. Let N be the kernel of f.Which of the following is FALSE? -
Let X1, X2, ..., Xn be an i.i.d. random sample from exponential distribution with mean μ. In other words, they have density
 Which of the following is NOT an unbiased estimate of μ?
Which of the following is NOT an unbiased estimate of μ? -
Let X1, X2, ..., Xn be an i.i.d. random sample from exponential distribution with mean μ. In other words, they have densityT(X) = (X1 + X2 + ...+ Xn)/(n+1)
 Consider the problem of estimating μ. The m.s.e (mean square error) of the estimateis
Consider the problem of estimating μ. The m.s.e (mean square error) of the estimateis -
Let X = {(x, y)∈â„2: x2 + y2 = 1} ∪ ([-1, 1] * {0}) ∪ ({0} * [-1, 1]). Let n0 = max{k: k < ∞, there are k distinct points p1,..., pk ∈ X such that X∖{p1,..., pk}is connected}The value of n0 is ______
-
Let X = {(x, y)∈â„2: x2 + y2 = 1} ∪ ([-1, 1] * {0}) ∪ ({0} * [-1, 1]). Let n0 = max{k: k < ∞, there are k distinct points p1,..., pk ∈ X such that X∖{p1,..., pk}is connected}Let q1,¦,qn0+1 be n0+1 distinct points and Y = X\{q1,¦,qn0+1}. Let m be the number of connected components of Y. The maximum possible value of m is ______
- A number is as much greater than 75 as it is smaller than 117. The number is:
-
The professor ordered to the students to go out of the class.I II III IVWhich of the above underlined parts of the sentence is grammatically incorrect?
-
Which of the following options is the closest in meaning to the word given below: Primeval
- Friendship, no matter how _________it is, has its limitations.


 Whatsapp
Whatsapp
 Facebook
Facebook

