GATE 2017-2018 :: GATE Mathematics
- For each λ > 0, let Xλ be a random variable with exponential density λe-λx on(0,∞). Then, Var(log Xλ)
- Let {an} be the sequence of consecutive positive solutions of the equation tan x = x and let {bn} be the sequence of consecutive positive solutions of the equation tan √x = x. Then
-
Let f be an analytic function on
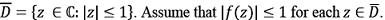 Then, which of the following is NOT a possible value of (ef)''(0)?
Then, which of the following is NOT a possible value of (ef)''(0)? -
Let V be the real vector space of all polynomials in one variable with real coefficients and having degree at most 20. Define the subspaces
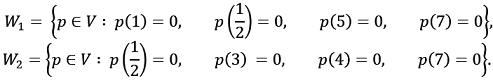 Then the dimension of W1∩W2 is ______
Then the dimension of W1∩W2 is ______ -
Let f, g : [0,1] →℠be defined by
 then
then -
Consider the following linear programming problem: Maximize x + 3y + 6z - wsubject to 5x + y + 6z + 7w ≤ 20,6x + 2y + 2z + 9w ≤ 40,x ≥ 0, y ≥ 0, z ≥ 0, w ≥ 0.Then the optimal value is ______
- Suppose X is a real-valued random variable. Which of the following values CANNOT be attained by E[X] and E[X2], respectively?
- Which of the following subsets of â„2 is NOT compact?
- Let ℋ be a Hilbert space and let {en : n ≥ 1} be an orthonormal basis of ℋ. Suppose T:ℋ → ℋ is a bounded linear operator. Which of the following CANNOT be true?


 Whatsapp
Whatsapp
 Facebook
Facebook


 .
.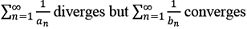 .
.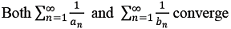 .
.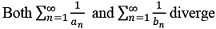 .
.