GATE 2017-2018 :: GATE Mathematics
- In a topological space, which of the following statements is NOT always true :
-
Consider the following statements: P: The family of subsets {An = (-1/n, 1/n), n = 1, 2, ...} satisfies the finite intersection property.Q: On an infinite set X , a metric d : X * X --> R is defined as d(x,y) = [0 , x = y and 1, x ≠y] The metric space (X,d) is compact.R: In a Frechet (T1) topological space, every finite set is closed.S: If f : R --> X is continuous, where R is given the usual topology and (X, t) is a Hausdorff (T2) space, then f is a one-one function.Which of the above statements are correct?
- A simple random sample of size 10 from 2 N(μ,σ2) gives 98% confidence interval (20.49, 23.51). Then the null hypothesis H0 : μ = 20.5 against HA : μ ≠20.5
-
For the linear programming problem Maximize z = x1 + 2x2 + 3x3 - 4x4Subject to 2x1 + 3x2 - x3 - x4 = 156x1 + x2 + x3 - 3x4 = 218x1 + 2x2 + 3x3 - 4x4 = 30x1, x2, x3, x4 ≥ 0,x1 = 4, x2 = 3, x3 = 0, x4 = 2 is
- Which one of the following statements is TRUE?
- Let V = ℂ2 be the vector space over the field of complex numbers and B{(1, i), (i,1)}be a given ordered basis of V. Then for which of the following, B* = {f1, f2}is a dual basis of B over ℂ?
- Let R = ℤ*ℤ*ℤ and I = ℤ*ℤ*{0}. Then which of the following statement is correct?
-
The function u(r, θ) satisfying the Laplace equation
 subject to the conditions u(e, θ) = 1, u(e2 ,θ) = 0 is
subject to the conditions u(e, θ) = 1, u(e2 ,θ) = 0 is -
If a transformation y = uv transforms the given differential equation f(x)y'' - 4f'(x)y' + g(x)y = 0 into the equation of the form v'' + h(x)v = 0, then u must be


 Whatsapp
Whatsapp
 Facebook
Facebook


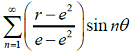 .
.