GATE 2017-2018 :: GATE Mathematics
- Let f : ℂ\{3i}→ℂ be defined by f(z) = (z-i)/(iz+3). Which of the following statements about f is FALSE?
-
The matrix A=
 can be decomposed uniquely into the product A = LU, where
can be decomposed uniquely into the product A = LU, where 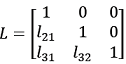 and
and  The solution of the system LX = [1 2 2]t is
The solution of the system LX = [1 2 2]t is - The image of the region {z ∈ℂ∶ Re(z)>Im(z)>0} under the mapping z↦(ez)2 is
- Let X be an arbitrary random variable that takes values in{0,1,¦,10}. The minimum and maximum possible values of the variance of X are
- Let M be the space of all 4*3 matrices with entries in the finite field of three elements. Then the number of matrices of rank three in M is
- Let V be a vector space of dimension m≥2. Let T:V → V be a linear transformation such that T<n+1 = 0 and T<n ≠0 for some n≥1. Then which of the following is necessarily TRUE?
- Let X be a convex region in the plane bounded by straight lines. Let X have 7 vertices. Suppose f(x,y) = ax + by + c has maximum value M and minimum value N on X and N < M. Let S = {P ∶ P is a vertex of X and N < f(P) < M}. If S has n elements, then which of the following statements is TRUE?
-
Which of the following statements are TRUE?P: If f∈L1(â„), then F is continuous.Q: If f∈L1(â„) and lim|x|→∞f(x) exists, then the limit is zero.R: If f∈L1(â„), then f is bounded.S: If f∈L1(â„) is uniformly continuous, then lim|x|→∞f(x) exists and equals zero.
-
Let u be a real valued harmonic function on â„‚. Let g:â„2 → â„ be defined by
 Which of the following statements is TRUE?
Which of the following statements is TRUE? - Let S = {z ∈ ℂ∶ |z|=1} with the induced topology from ℂ and let f:[0,2] → S be defined as f(t) = e2πit. Then, which of the following is TRUE?


 Whatsapp
Whatsapp
 Facebook
Facebook

