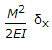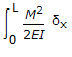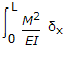Menu
Home / Civil Engineering / Theory of Structures :: Section 1

Civil Engineering :: Theory of Structures

Theory of Structures - Section 1
Theory of Structures - Section 2
Theory of Structures - Section 3
Theory of Structures - Section 4
Theory of Structures - Section-5

  1. Stress may be expressed in Newtons
    2. A.

    per millimetre square (N/mm2)
    B.

    per centimetre square (N/cm2)
    C.

    per metre square (N/m2)
    D.

    All of the above.

    View Answer

    Workspace

    Discuss Discuss in Forum

  2. Principal planes are subjected to

    3. A.

    normal stresses only
    B.

    tangential stresses only
    C.

    normal stresses as well as tangential stresses
    D.

    none of these.

    View Answer

    Workspace

    Discuss Discuss in Forum

  3. In plastic analysis, the shape factor for a circular section, is
    4. A.

    1.5
    B.

    1.6
    C.

    1.7
    D.

    1.75

    View Answer

    Workspace

    Discuss Discuss in Forum

  4. Keeping the depth d constant, the width of a cantilever of length l of uniform strength loaded with a uniformly distributed load w varies from zero at the free end and
    5. A.

    \(\frac { 2w } { \sigma d^2} *I^2\) at the fixed end
    B.

    \(\frac { 3w } { \sigma d} *I^2\)at the fixed end
    C.

    \(\frac { 3w } { \sigma d^2} *I^2\)at the fixed end
    D.

    \(\frac { 5w } { \sigma d} *I^2\)at the fixed end

    View Answer

    Workspace

    Discuss in Forum

  5. The total strain energy of a beam of length L, having moment of inertia of its section I, when subjected to a bending moment M, is

    6. A.

    \( \frac { M^2 } { EI } \)
    B.

    C.

    D.

    View Answer

    Workspace

    Discuss in Forum

  6. A load of 1960 N is raised at the end of a steel wire. The minimum diameter of the wire so that stress in the wire does not exceed 100 N/mm2 is :

    7. A.

    4.0 mm
    B.

    4.5 mm
    C.

    5.0 mm
    D.
    5.5 mm
    E.

    6.0 mm

    View Answer

    Workspace

    Discuss Discuss in Forum

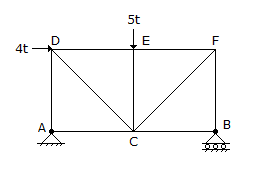
  7. The force in BF of the truss shown in given figure, is

    8. A.

    4t tension
    B.

    4t compression
    C.

    4.5t tension
    D.

    4.5t compression
    E.

    zero.

    View Answer

    Workspace

    Discuss in Forum

  8. The radius of gyration of a section of area A and least moment of inertia I about the centroidal axis, is
    9. A.

    \(\frac { A } { I} \)
    B.

    \(\frac { I} { A} \)
    C.

    \( \sqrt\frac { I } {A } \)
    D.

    \( \sqrt\frac { A } {I} \)

    View Answer

    Workspace

    Discuss in Forum

  9. A simply supported beam carries varying load from zero at one end and w at the other end. If the length of the beam is a, the maximum bending moment will be
    10. A.

    \( \frac { wa} { 2 7} \)
    B.

    \( \frac { wa^2} { 27} \)
    C.

    \( \frac { w^2a} { \sqrt{ 27}} \)
    D.

    \( \frac { w^2a} { 9\sqrt{ 3}} \)

    View Answer

    Workspace

    Discuss in Forum

  10. A simply supported beam carries varying load from zero at one end and w at the other end. If the length of the beam is a, the maximum bending moment will be
    11. A.

    \( \frac { wa} { 2 7} \)
    B.

    \( \frac { wa^2} { 27} \)
    C.

    \( \frac { w^2a} { \sqrt{ 27}} \)
    D.

    \( \frac { w^2a} { 9\sqrt{ 3}} \)

    View Answer

    Workspace

    Discuss in Forum

Java Programming Questions and Answers Interview Questions and Answers