GATE 2017-2018 :: GATE Physics
-
The degenerate eigenvalue of the matrix
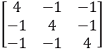is (your answer should be an integer) _________________ -
Consider the decay of a pion into a muon and an anti-neutrino π- → μ- + v-μ in the pion rest frame. mπ = 139.6 MeV/c2, mμ = 105.7 MeV/c2, mv ≈ 0The energy (in MeV) of the emitted neutrino, to the nearest integer is ____________
-
In a constant magnetic field of 0.6 Tesla along the z direction, find the value of the path integral
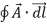in the units of (Tesla m2) on a square loop of side length (1/ √2 ) meters. The normal to the loop makes an angle of 60° to the z-axis, as shown in the figure. The answer should be up to two decimal places. ____________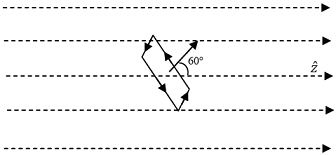
- A spin-half particle is in a linear superposition 0.8|↑〉 + 0.6|↓〉 of its spin-up and spin-down states. If |↑〉 and |↓〉 are the eigenstates of σz then what is the expectation value, up to one decimal place, of the operator 10σz + 5σx ? Here, symbols have their usual meanings. ____________
- Consider the wave function Aeikr (r0/r) where 􀜣 is the normalization constant. For r = 2r0, the magnitude of probability current density up to two decimal places, in units of (A2ћk/m), is
- An n-channel junction field effect transistor has 5mA source to drain current at shorted gate (IDSS) and 5V pinch off voltage (VP). Calculate the drain current in mA for a gate-source voltage (VGS) of -2.5V. The answer should be up to two decimal places. ________________
-
There are four energy levels E, 2E, 3E and 4E (where E >0). The canonical partition function of two particles is , if these particles are two identical fermions
-
There are four energy levels E, 2E, 3E and 4E (where E >0). The canonical partition function of two particles is , if these particles are two distinguishable particles
-
To the given unperturbed Hamiltonian
we add a small perturbation given by
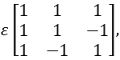where ϵ is a small quantity.The ground state eigenvector of the unperturbed Hamiltonian is -
To the given unperturbed Hamiltonianwe add a small perturbation given by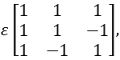where ϵ is a small quantity.A pair of eigenvalues of the perturbed Hamiltonian, using first order perturbation theory, is
Whatsapp
Facebook
