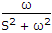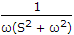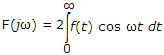ECE :: Signals and Systems
-
If average correlation between v1(t) and v2(t) is R12(t) and average correlation between v2(t) and v1(t) is R21(t) then
-
A stationary process has
-
Algebraic expression for z-transform of x[n] is X[z]... What is the algebraic expression of z-transform of ejω0n x[n]?
-
The waveform shown in the given Figure can be written as
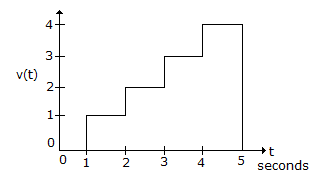
-
Assertion (A): The function δ'(t - b) is equal to 0 for t ≠ b
Reason (R): A number of impulses spaced from one another form an impulse train.
-
The range of values of a and b for which the linear time invariant system with impulse response.
h(n) = an n ≥ 0
= bn n < 0
will be stable if



 Whatsapp
Whatsapp
 Facebook
Facebook