Discussion :: Time and Work
-
In how many days can 10 women finish a work?
I .10 men can complete the work in 6 days.
II.10 men and 10 women together can complete the work in \(\left(\frac{33}{7}\right)\) days.
III.If 10 men work for 3 days and thereafter 10 women replace them, the remaining work in completed in 4 days.
Answer : Option A
Explanation :
I. (10 x 6) men can complete the work in 1 day.
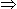 1 man's 1 day's work =\(\frac { 1 } { 60 }\)
1 man's 1 day's work =\(\frac { 1 } { 60 }\)
II.\( [10*\frac { 24} {7 } ]\)men +\( [10*\frac { 24} {7 } ]\)women can complete the work in 1 day
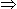 \(( \frac {2 40 } { 7} )\)men's 1 day work +\(( \frac {2 40 } { 7} )\)women's 1 day work = 1
\(( \frac {2 40 } { 7} )\)men's 1 day work +\(( \frac {2 40 } { 7} )\)women's 1 day work = 1
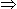 \([ \frac {2 40 } { 7} \)\(*\frac {1} {60 } ]\)+\(( \frac {2 40 } { 7} )\)women's 1 day's work = 1
\([ \frac {2 40 } { 7} \)\(*\frac {1} {60 } ]\)+\(( \frac {2 40 } { 7} )\)women's 1 day's work = 1
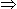 \(( \frac {2 40 } { 7} )\)women's 1 day's work =[1-\(\frac { 4 } { 7 } \)]=\(\frac {3 } { 7 } \)
\(( \frac {2 40 } { 7} )\)women's 1 day's work =[1-\(\frac { 4 } { 7 } \)]=\(\frac {3 } { 7 } \)
 10 women's 1 day's work =[\(\frac {3 } { 7 } *\)\(\frac {7 } { 240 } *10]\)=\(\frac { 1 } { 8 } \)
10 women's 1 day's work =[\(\frac {3 } { 7 } *\)\(\frac {7 } { 240 } *10]\)=\(\frac { 1 } { 8 } \)
So, 10 women can finish the work in 8 days.
III. (10 men's work for 3 days) + (10 women's work for 4 days) = 1
 (10 x 3) men's 1 day's work + (10 x 4) women's 1 day's work = 1
(10 x 3) men's 1 day's work + (10 x 4) women's 1 day's work = 1
 30 men's 1 day's work + 40 women's 1 day's work = 1
30 men's 1 day's work + 40 women's 1 day's work = 1
Thus, I and III will give us the answer.
And, II and III will give us the answer.
Be The First To Comment


 Whatsapp
Whatsapp
 Facebook
Facebook

