Discussion :: Surds and Indices
-
If x = 3 +2 \(\sqrt{2} \), then the value of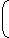 
\(\sqrt{X} \) - 1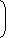 
is: \(\sqrt{X} \)\(\)
Whatsapp
Facebook
Answer : Option B
Explanation :
\( [\sqrt{x}-\)\( \frac { 1 } { \sqrt{X} } )^2\)=X+\( \frac { 1 } { X } -2\)
=(3+\(2\sqrt{2}\))+\( \frac { 1 } {(3+2€‹€‹€‹€‹€‹€‹ \sqrt{2)}} -2\)
=(3+\(2\sqrt{2}\))+\( \frac { 1 } {(3+2€‹€‹€‹€‹€‹€‹ \sqrt{2)}} \)*\(\frac {( 3-€‹€‹€‹€‹2 \sqrt{2})} { (3-2\sqrt{2} )} -2\)
=(3+\(2\sqrt{2}\))+(3-\(2\sqrt{2}\))-2
=4
[\(\sqrt{X}\)-\(\frac { 1 } { \sqrt{X} }\)]=2
Be The First To Comment