Arithmetic Aptitude :: Problems on H.C.F and L.C.M
-
The least number which should be added to 2497 so that the sum is exactly divisible by 5, 6, 4 and 3 is:
-
Reduce \(\frac { 128352 } { 238368 } \)to its lowest terms.
-
The least number which when divided by 5, 6 , 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder, is:
-
A, B and C start at the same time in the same direction to run around a circular stadium. A completes a round in 252 seconds, B in 308 seconds and c in 198 seconds, all starting at the same point. After what time will they again at the starting point ?
-
The H.C.F. of two numbers is 11 and their L.C.M. is 7700. If one of the numbers is 275, then the other is:
-
What will be the least number which when doubled will be exactly divisible by 12, 18, 21 and 30 ?
-
The smallest number which when diminished by 7, is divisible 12, 16, 18, 21 and 28 is:
-
252 can be expressed as a product of primes as:
Whatsapp
Facebook
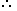Number to be added = (60 - 37) = 23.