Probability - Arithmetic Aptitude Questions and Answers

Home / Arithmetic Aptitude / Probability :: Discussion

A bag contains 4 white, 5 red and 6 blue balls. Three balls are drawn at random from the bag. The probability that all of them are red, is:

$\frac { 1 } { 22 }$

$\frac { 3 } { 22 }$

$\frac { 2 } { 21 }$

$\frac { 2 } {77 }$

Answer : Option C

Explanation :

Let S be the sample space.

Then, n(S)	= number of ways of drawing 3 balls out of 15
	= ¹⁵C₃

= $\frac { (15*14*13) } { (3*2*1) }$

= 455

Let E = event of getting all the 3 red balls.

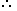n(E) = ⁵C₃ = ⁵C₂ = $\frac { (5*1) } { (2 *1)}$ =10

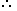P(E) = $\frac { n(E) } { n(S)}$ = $\frac { 10 } { 455 }$ = $\frac { 2 } { 21 }$

Psr said : (Jan 22, 2022)

10/455 is 2/91.

Comments

Name