Discussion :: Pipes and Cistern
-
Three pipes A, B and C can fill a tank in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 7 hours. The number of hours taken by C alone to fill the tank is:
Whatsapp
Facebook
Answer : Option C
Explanation :
Part filled in 2 hours =\( \frac { 2 } { 6 }\)=\( \frac {1 } { 3 }\)
Remaining part =[1-\( \frac {1 } { 3 }\)]=\( \frac {2 } { 3 }\)
(A + B)'s 7 hour's work =\( \frac {2 } { 3 }\)
(A + B)'s 1 hour's work =\( \frac {2 } { 21 }\)
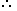C's 1 hour's work = { (A + B + C)'s 1 hour's work } - { (A + B)'s 1 hour's work }
=[\( \frac { 1 } {6} \)-\( \frac {2 } { 21 }\)] =\( \frac { 1 } {14} \)
C alone can fill the tank in 14 hours.
Be The First To Comment