Trigonometry:

In a right angled  OAB, where BOA = ,

i.   sin  =\(\frac { Perpendicular } { Hypotenuse }\)		=\(\frac { AB } { OB } \)		;

ii.   cos  =\(\frac { Base } { Hypotenuse } \)		= \(\frac { OA } { OB } \)		;

iii.  tan  =		\(\frac { Perpendicular } { Base } \)=		\(\frac { AB } { OA } \);

iv.  cosec  =\(\frac { 1 } { sin\theta } \)		=\(\frac { OB } { OA }\)		;

v.   sec  =		\(\frac { 1 } { cos\theta } \)=		\(\frac { OA } { AB } \);

vi.  cot  =		\(\frac { 1 } { tan\theta }\)=		\(\frac { OA } { AB }\);

Trigonometrical Identities:

1. sin²  + cos²  = 1.

2. 1 + tan²  = sec² .

3. 1 + cot²  = cosec² .

Values of T-ratios:

	0°	(/6) 30°	(/4) 45°	(/3) 60°	(/2) 90°
sin	0		\(\frac { 1 } { 2 } \)	\(\frac { 3 } { 2 } \)	1
cos	1	\( \frac { 3 } { 2 } \)	\(\frac { 1 } { 2 } \)		0
tan	0	\(\frac { 1 } { 3 } \)	1	3	not defined

Angle of Elevation:

Suppose a man from a point O looks up at an object P, placed above the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the angle of elevation of P as seen from O.

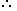 Angle of elevation of P from O = AOP.

Angle of Depression:

Suppose a man from a point O looks down at an object P, placed below the level of his eye, then the angle which the line of sight makes with the horizontal through O, is called the angle of depression of P as seen from O.