Discussion :: Height and Distance
-
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. respectively. If the lighthouse is 100 m high, the distance between the two ships is:
Answer : Option C
Explanation :
Let AB be the lighthouse and C and D be the positions of the ships.
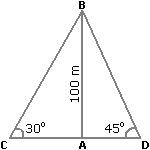
Then, AB = 100 m, 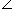 ACB = 30° and
ACB = 30° and 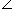 ADB = 45°.
ADB = 45°.
| \( \frac { AB } { AC } \)= tan 30° = | \(\frac { 1 } { 3 }\)  AC = AB x 3 = 1003 m. AC = AB x 3 = 1003 m. |
||
\(\frac { AB } { AD } \)= tan 45° = 1 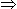 AD = AB = 100 m. AD = AB = 100 m. |
|
 CD = (AC + AD) CD = (AC + AD) |
= (1003 + 100) m |
| = 100(3 + 1) | |
| = (100 x 2.73) m | |
| = 273 m. |
Be The First To Comment


 Whatsapp
Whatsapp
 Facebook
Facebook
