GATE 2017-2018 :: GATE ECE
- With initial condition x(1) = 0.5 , the solution of the differential equation, t dx/dt + x = t is
-
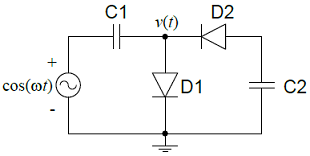
The diodes and capacitors in the circuit shown are ideal. The voltage v(t) across the diode D1 is
- A source alphabet consists of N symbols with the probability of the first two symbols being the same. A source encoder increases the probability of the first symbol by a small amount ε and decreases that of the second by ε . After encoding, the entropy of the source
-
The radiation pattern of an antenna in spherical co-ordinates is given byF(θ) = cos4 θ; 0 ≤ θ ≤ π /2The directivity of the antenna is
- If x[n] = (1/3)|n| - (1/ 2)n u[n], then the region of convergence (ROC) of its Z-transform in the Z-plane will be
- In the sum of products function f (X, Y, Z) = Σ(2, 3, 4, 5) , the prime implicants are
-
A system with transfer functionG(s) = [(s2 + 9)(s + 2)] / [(s + 1)(s + 3)(s + 4)]is excited by sin(w t) . The steady-state output of the system is zero at
-
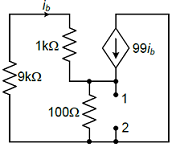
The impedance looking into nodes 1 and 2 in the given circuit is
-
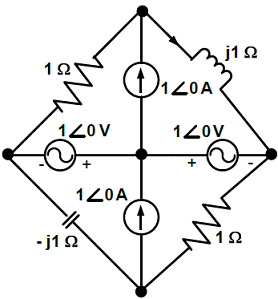
In the circuit shown below, the current through the inductor is
-
Given f(z) = 1/(z + 1) - 2/(z + 3). If C is a counterclockwise path in the z-plane such that |z + 1| = 1 the value of
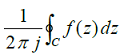is
Whatsapp
Facebook
.
.
.
.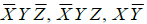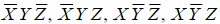